krone
VIP Members
-
26/07/2016
-
141
-
259 bài viết
Kiến trúc mã hoá khối (Block Cipher) – P1
Mã hoá khối truyền thống
Một số thuật toán mã hóa khối đối xứng quan trọng được sử dụng hiện tại được dựa trên cấu trúc được gọi là mật mã khối Feistel [FEIS73]. Vì lý do đó, điều quan trọng là kiểm tra các nguyên tắc thiết kế của mật mã Feistel. Chúng ta bắt đầu với một so sánh về Stream Cipher và Block Cipher. Sau đó, chúng ta thảo luận về cấu trúc mật mã khối Feistel.

Stream Ciphers và Block Ciphers
Stream Cipher là loại mã hóa luồng dữ liệu số một bit hoặc một byte mỗi lần. Ví dụ về stream cipher cổ điển là mật mã Vigenère tự động và mật mã Vernam. Trong trường hợp lý tưởng, phiên bản one-time pad. của mật mã Vernam sẽ được sử dụng, trong đó keystream (ki) dài bằng số bit plaintext (pi). Nếu keystream mật mã là ngẫu nhiên, thì mật mã này không thể bị phá vỡ bằng bất kỳ phương tiện nào khác ngoài việc có được keystream. Tuy nhiên, keystream phải được cung cấp cho cả hai phía người dùng trước thông qua một số kênh độc lập và an toàn. Điều này dẫn đến một số vấn đề không thể sử dụng đối với dữ liệu lớn
Theo đó, vì lý do thực tế, trình tạo bit-stream phải được xem là một thủ tục thuật toán, vì vậy bit-stream mã hoá có thể được sản xuất bởi cả hai phía người dùng. Bộ tạo bit-stream là một thuật toán được điều khiển bằng khóa và phải tạo ra một bit-stream mạnh về mặt mã hoá. Nghĩa là, phải tính toán không thực tế để dự đoán các phần trong tương lai của bit-stream dựa trên các phần trước của bit-stream. Hai người dùng chỉ cần chia sẻ khóa tạo và mỗi người có thể tạo ra keystream.
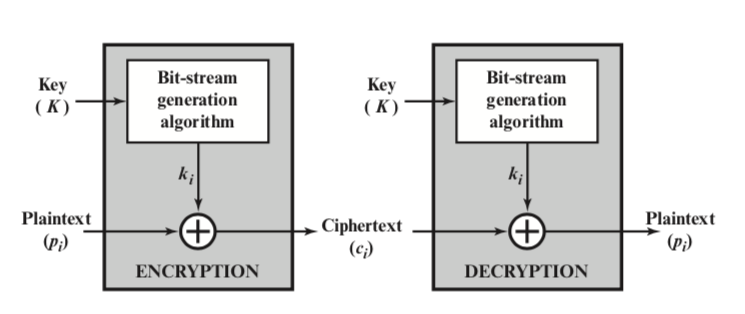
Block Cipher là một khối trong đó một khối plaintext được coi là khối văn bản gốc cần được xử lý và được sử dụng để tạo ra một khối cipher text có độ dài bằng nhau. Thông thường, kích thước khối 64 hoặc 128 bit được sử dụng, giống như với Stream Cipher, hai người dùng chia sẻ khóa mã hóa đối xứng.
Sử dụng một số chế độ hoạt động, một Block Cipher có thể được sử dụng để đạt được hiệu quả tương tự như Stream Cipher. Cần nhiều nỗ lực hơn nữa để đi vào phân tích mật mã khối, nhìn chung, Block cipher dường như có thể áp dụng cho một phạm vi ứng dụng rộng hơn so với Stream Cipher. Phần lớn các ứng dụng mã hóa đối xứng dựa trên mạng sử dụng Block Cipher.
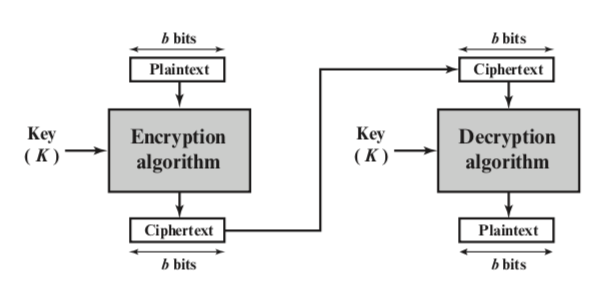
Cấu trúc mật mã Feistel
Một mật mã khối hoạt động trên một khối plaintext gồm n bit để tạo ra một khối ciphertext gồm n bit. Có 2^n khối plaintext khác nhau có thể và để mã hóa có thể đảo ngược (nghĩa là để giải mã được), mỗi khối phải tạo ra một khối ciphertext duy nhất. Một chuyển đổi như vậy được gọi là đảo ngược, hoặc không có nghĩa. Các ví dụ sau đây minh họa các phép biến đổi không đặc trưng và số ít cho n = 2.
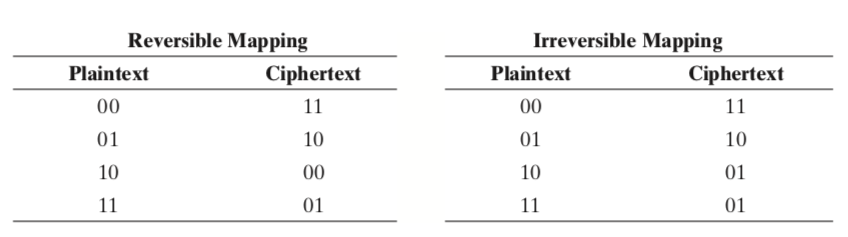
Trong trường hợp sau, một ciphertext của 01 có thể được tạo bởi một trong hai khối văn bản thuần túy. Vì vậy, nếu chúng ta giới hạn reversible mapping, số lượng biến đổi khác nhau là (2n!)^2.
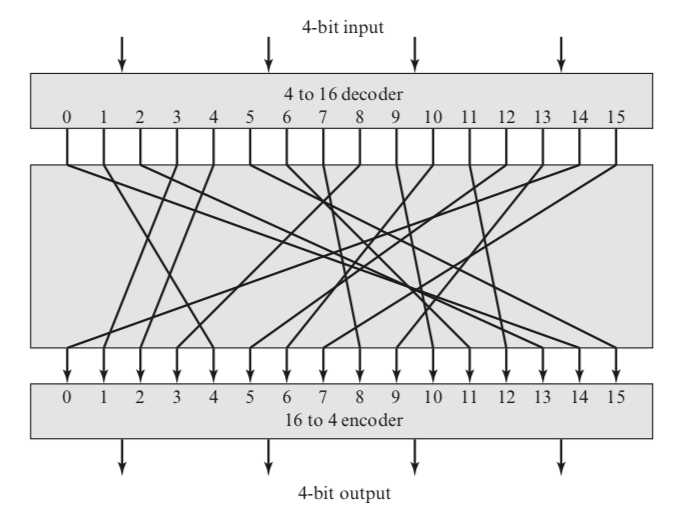
Hình trên minh họa logic của một mật mã thay thế chung cho n = 4. Một đầu vào 4 bit tạo ra một trong 16 trạng thái đầu vào có thể, được ánh xạ bởi mật mã phụ vào một trong 16 trạng thái đầu ra có thể, mỗi trạng thái được lặp lại - được gửi bởi 4 bit plaintext.
Ánh xạ mã hóa và giải mã có thể được xác định bằng cách lập bảng, như bảng dưới đây:
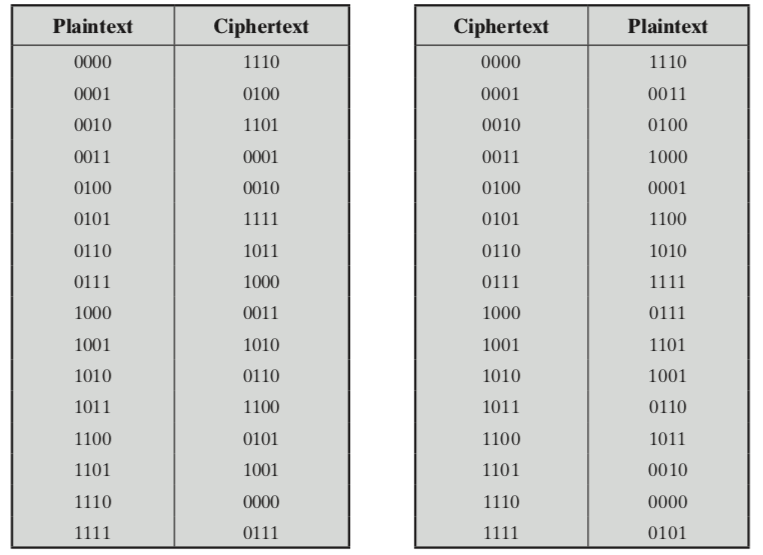
Feistel gọi đây là “idea block cipher”. Bởi vì nó cho phép số lượng ánh xạ mã hóa tối đa có thể có từ khối plaintext. Nhưng có một vấn đề thực tế với “idea block cipher”. Nếu kích thước khối nhỏ, chẳng hạn như n = 4, được sử dụng, thì hệ thống tương đương với mật mã thay thế cổ điển. Các hệ thống như vậy, như chúng ta đã thấy, dễ bị tấn công khi phân tích thống kê về plaintext. Điểm yếu này không phải là cố hữu trong việc sử dụng mật mã thay thế mà là kết quả của việc sử dụng kích thước khối nhỏ. Nếu n đủ lớn và sự thay thế có thể đảo ngược tùy ý giữa plaintext và cipher được cho phép, thì các đặc điểm thống kê của plaintext gốc được che giấu đến mức mà loại phân tích mật mã này không khả thi. Tuy nhiên, một mật mã thay thế có thể đảo ngược tùy ý (mật mã khối lý tưởng) cho kích thước khối lớn là không thực tế, tuy nhiên, từ quan điểm thực hiện và hiệu suất. Đối với một chuyển đổi như vậy, chính ánh xạ tạo thành khóa. Xem xét lại bảng chuyển đổi phía trên, định nghĩa một ánh xạ đảo ngược cụ thể từ plaintext sang ciphertext cho n = 4. Ánh xạ có thể được xác định bởi các mục trong cột thứ hai, hiển thị giá trị của ciphertext cho mỗi khối plaintext. Về bản chất, đây là chìa khóa xác định ánh xạ cụ thể trong số tất cả các ánh xạ có thể. Trong trường hợp này, sử dụng phương pháp xác định khóa đơn giản này, độ dài khóa cần thiết là (4 bit) * (16 rows) = 64 bit. Nói chung, đối với một mật mã khối lý tưởng n bit, độ dài của khóa được xác định theo kiểu này là n * (2^n) bit. Đối với khối 64 bit, có độ dài mong muốn để ngăn chặn các cuộc tấn công thống kê, độ dài khóa cần thiết là 64 * (2^64) = 2^70 tương đương 10^21 bit.
Một số thuật toán mã hóa khối đối xứng quan trọng được sử dụng hiện tại được dựa trên cấu trúc được gọi là mật mã khối Feistel [FEIS73]. Vì lý do đó, điều quan trọng là kiểm tra các nguyên tắc thiết kế của mật mã Feistel. Chúng ta bắt đầu với một so sánh về Stream Cipher và Block Cipher. Sau đó, chúng ta thảo luận về cấu trúc mật mã khối Feistel.
Stream Ciphers và Block Ciphers
Stream Cipher là loại mã hóa luồng dữ liệu số một bit hoặc một byte mỗi lần. Ví dụ về stream cipher cổ điển là mật mã Vigenère tự động và mật mã Vernam. Trong trường hợp lý tưởng, phiên bản one-time pad. của mật mã Vernam sẽ được sử dụng, trong đó keystream (ki) dài bằng số bit plaintext (pi). Nếu keystream mật mã là ngẫu nhiên, thì mật mã này không thể bị phá vỡ bằng bất kỳ phương tiện nào khác ngoài việc có được keystream. Tuy nhiên, keystream phải được cung cấp cho cả hai phía người dùng trước thông qua một số kênh độc lập và an toàn. Điều này dẫn đến một số vấn đề không thể sử dụng đối với dữ liệu lớn
Theo đó, vì lý do thực tế, trình tạo bit-stream phải được xem là một thủ tục thuật toán, vì vậy bit-stream mã hoá có thể được sản xuất bởi cả hai phía người dùng. Bộ tạo bit-stream là một thuật toán được điều khiển bằng khóa và phải tạo ra một bit-stream mạnh về mặt mã hoá. Nghĩa là, phải tính toán không thực tế để dự đoán các phần trong tương lai của bit-stream dựa trên các phần trước của bit-stream. Hai người dùng chỉ cần chia sẻ khóa tạo và mỗi người có thể tạo ra keystream.
Block Cipher là một khối trong đó một khối plaintext được coi là khối văn bản gốc cần được xử lý và được sử dụng để tạo ra một khối cipher text có độ dài bằng nhau. Thông thường, kích thước khối 64 hoặc 128 bit được sử dụng, giống như với Stream Cipher, hai người dùng chia sẻ khóa mã hóa đối xứng.
Sử dụng một số chế độ hoạt động, một Block Cipher có thể được sử dụng để đạt được hiệu quả tương tự như Stream Cipher. Cần nhiều nỗ lực hơn nữa để đi vào phân tích mật mã khối, nhìn chung, Block cipher dường như có thể áp dụng cho một phạm vi ứng dụng rộng hơn so với Stream Cipher. Phần lớn các ứng dụng mã hóa đối xứng dựa trên mạng sử dụng Block Cipher.
Một mật mã khối hoạt động trên một khối plaintext gồm n bit để tạo ra một khối ciphertext gồm n bit. Có 2^n khối plaintext khác nhau có thể và để mã hóa có thể đảo ngược (nghĩa là để giải mã được), mỗi khối phải tạo ra một khối ciphertext duy nhất. Một chuyển đổi như vậy được gọi là đảo ngược, hoặc không có nghĩa. Các ví dụ sau đây minh họa các phép biến đổi không đặc trưng và số ít cho n = 2.
Ánh xạ mã hóa và giải mã có thể được xác định bằng cách lập bảng, như bảng dưới đây:
Chỉnh sửa lần cuối bởi người điều hành: