Dior
New Member
-
19/11/2020
-
6
-
3 bài viết
Các chuẩn mã hóa sử dụng trong chữ ký số
Nhắc đến chữ ký số, chúng ta sẽ nghĩ đến việc sử dụng mật mã khóa công khai tạo ra cặp khóa công khai - bí mật để mã hóa và giải mã. Vậy cặp khóa công khai - bí mật được tạo ra như thế nào? Bài viết này chúng ta sẽ tìm hiểu về một số giải thuật dùng để sinh cặp khóa trong chữ ký số.
 Hệ mật RSA
Hệ mật RSA
RSA là hệ mã hoá bất đối xứng được đặt theo tên của 3 nhà phát triển ra nó là Ron Rivest, Adi Shamir và Leonard Adleman, đây là thuật toán đầu tiên phù hợp với việc tạo ra chữ ký điện tử và việc mã hóa. Nó đánh dấu một sự tiến bộ vượt bậc của lĩnh vực mật mã học trong việc sử dụng khóa công cộng.
RSA vẫn rất phổ biến do độ dài khóa của nó. Một khóa RSA thường dài 1024 hoặc 2048 bit. Tuy nhiên, theo các chuyên gia bảo mật thì không mất nhiều thời gian để crack RSA 1024 bit, do đó nhiều tổ chức phải chuyển sang khóa 2048 bit mạnh mẽ hơn.
Hệ mật ECC (Elliptic Curve Cryptography)
Bên cạnh hệ mật RSA còn có một giải thuật khóa công khai được các chuyên gia khuyên dùng là ECC - hệ mật dựa trên đường cong Elliptic
ECC được sử dụng trong nhiều ứng dụng: chính phủ Mỹ dùng ECC để bảo vệ thông tin liên lạc nội bộ, các dự án Tor sử dụng để giúp đảm bảo ẩn danh, đây cũng là cơ chế được sử dụng để chứng minh quyền sở hữu trong Bitcoins, cung cấp chữ ký số trong dịch vụ iMessage của Apple, để mã hóa thông tin DNS với DNSCurve và là phương pháp tốt để xác thực cho các trình duyệt web an toàn qua SSL/TLS.
ECDSA (Thuật toán Chữ ký số Elliptic Curve) dựa trên DSA là một phần của mật mã đường cong Elliptic. Chính thuật toán ECDSA đã làm hệ mật ECC trở nên hữu ích cho bảo mật.
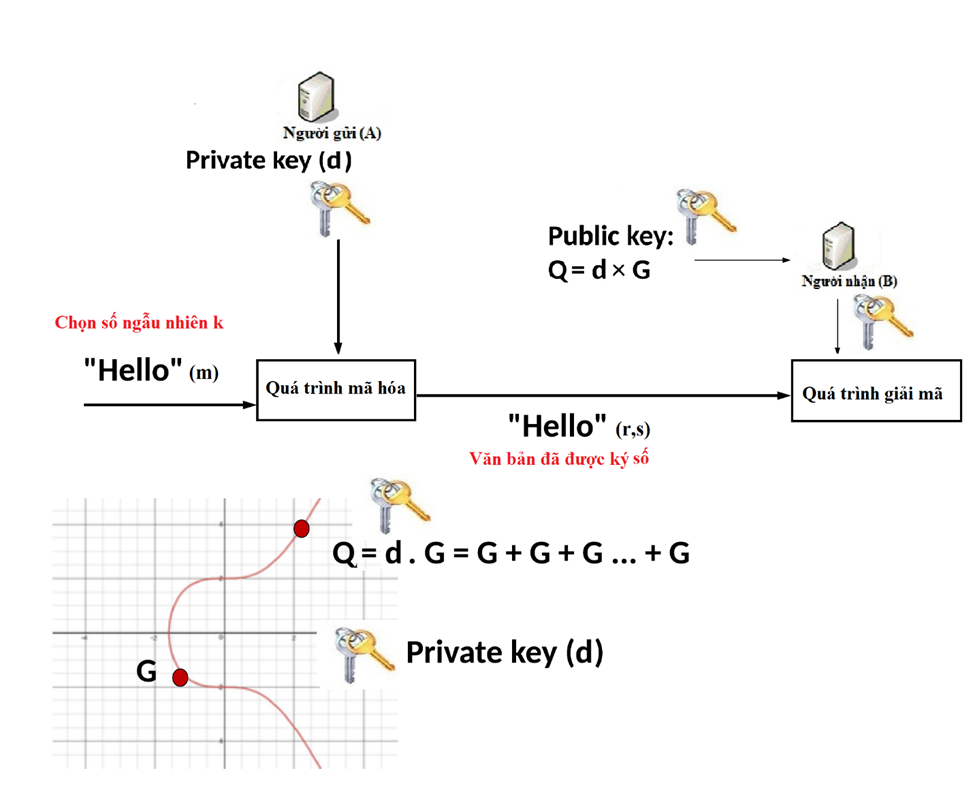
Hình 2. Mô hình sử dụng thuật toán mã hóa ECC trong chữ ký số
Dưới đây là mô tả chi tiết về quá trình mã hóa và giải mã trong mô hình trên.
Thuật toán ký trên bản rõ m (Quá trình mã hóa)
Người dùng A ký lên thông điệp m theo các bước sau:
Thuật toán kiểm tra chữ ký (Quá trình giải mã)
Người dùng B kiểm tra chữ ký (r,s) trên thông điệp m theo các bước sau:
Hiện nay, hệ mật RSA là giải thuật khoá công khai được sử dụng phổ biến nhất, nhưng hệ mật dựa trên đường cong Elliptic (ECC) có thể thay thế cho RSA bởi mức an toàn và tốc độ xử lý cao hơn.
Dưới đây, là bảng so sánh các kích thước khóa RSA và ECDSA với cùng mức độ bảo mật.
Chú thích :
Rõ ràng với mức độ bảo mật như nhau thì độ dài khóa của ECDSA là nhỏ hơn so với RSA. Từ đó làm tăng tốc độ xử lý một cách đáng kể, do số phép toán dùng để mã hoá và giải mã ít hơn và yêu cầu các thiết bị có khả năng tính toán thấp hơn, nên giúp tăng tốc độ và làm giảm năng lượng cần sử dụng trong quá trình mã hoá và giải mã.
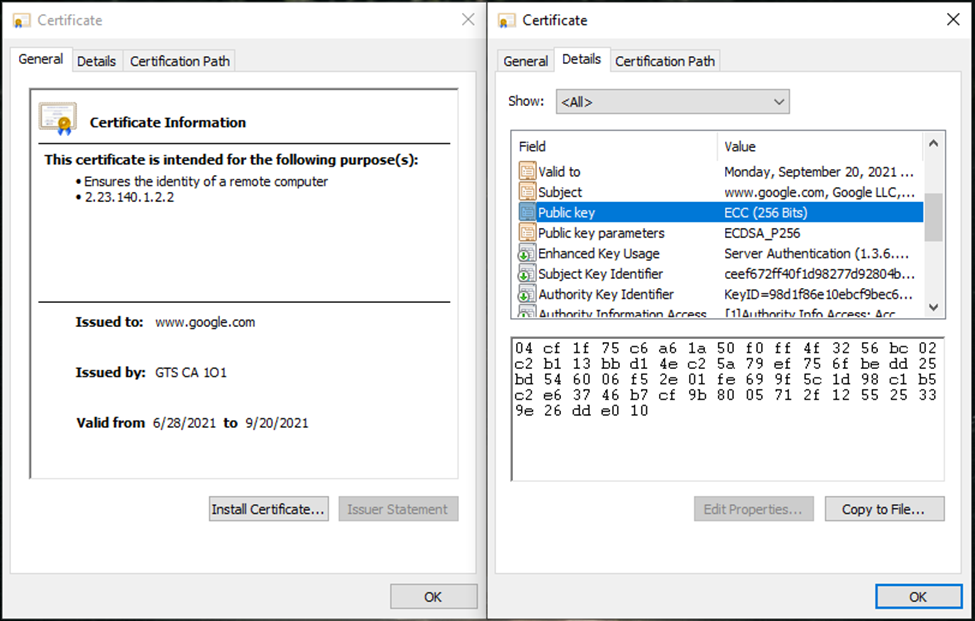
Hình 3. Chứng thư số của trang web google.com.vn
Dễ dàng thấy được sự cải tiến của của ECDSA khiến hiệu suất của loại mã khóa này tốt hơn hẳn so với RSA, với sự cải thiện này chỉ một vài năm tới ECC sẽ là giải thuật trao đổi khoá công khai được sử dụng phổ biến nhất. Có thể nói ECC chính là hệ mật mạnh nhất hiện nay và cũng là ứng viên sáng giá để thay thế RSA trong việc tạo ra các khóa mã ngắn hơn mà vẫn đảm bảo an toàn.
Trên đây là hai loại hệ mật được sử dụng phổ biến trong việc tạo lập một chữ ký số và cả hai hê mật này đều có mức độ bảo mật cao mà các hacker ngày nay khó có thể thâm nhập được. Mong rằng bài viết này sẽ giúp các bạn có cái nhìn tổng quát hơn về RSA và ECC. Hẹn gặp các bạn trong những bài viết tiếp theo.
RSA là hệ mã hoá bất đối xứng được đặt theo tên của 3 nhà phát triển ra nó là Ron Rivest, Adi Shamir và Leonard Adleman, đây là thuật toán đầu tiên phù hợp với việc tạo ra chữ ký điện tử và việc mã hóa. Nó đánh dấu một sự tiến bộ vượt bậc của lĩnh vực mật mã học trong việc sử dụng khóa công cộng.
- Thuật toán sinh khóa RSA tuân theo chuẩn PKCS#1và được mô tả như sau:
1. Chọn 2 số p, q . Trong đó p và q là số nguyên tố
2. Tính n = p*q
3. Tính: giá trị hàm số Euler Ø(n) = (p-1)*(q-1)
4. Chọn một số tự nhiên e sao cho 1 < e < Ø(n) và là số nguyên tố cùng nhau với Ø(n).
5. Tính d = (e^(-1)) mod Ø(n)
6. Khi đó khóa công khai: KU = [e,n]
7. Khóa bí mật: KR = [d,n]
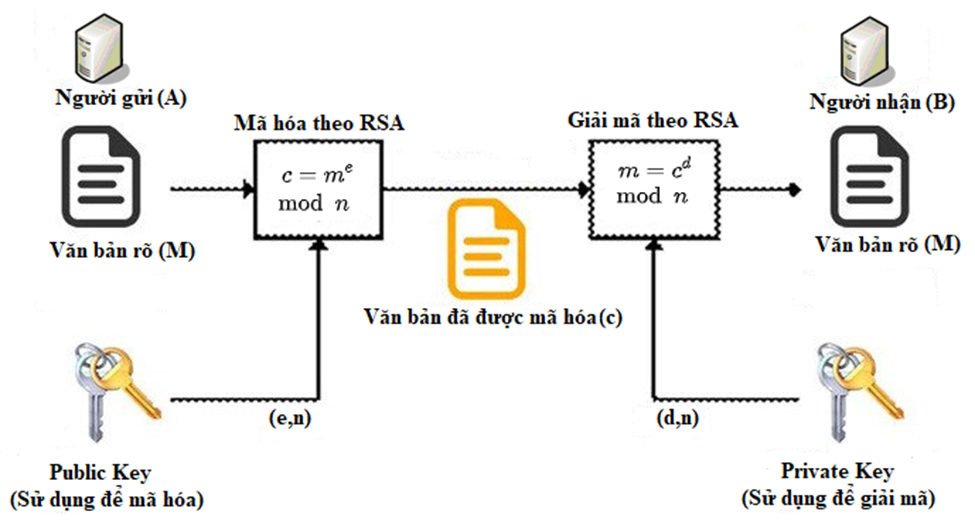
Hình 1. Mô hình trao đổi thông tin sử dụng thuật toán mã hóa RSA
- Trong mô hình trên giả sử A muốn gửi đoạn thông tin M cho B.
Đầu tiên A chuyển M thành một số m < n theo một hàm có thể đảo ngược (từ m có thể xác định lại M) được thỏa thuận trước.
- Lúc này A có m và biết n cũng như e (e trong Public Key) do B gửi. A sẽ tính c là bản mã hóa của m theo công thức: c=(m^e) mod n
- Khi B nhận c từ A và biết khóa bí mật d. A có thể tìm được m từ c theo công thức sau: m= (c^d) mod n
- Sau khi biết m, B tìm lại M theo phương pháp đã thỏa thuận trước.
RSA vẫn rất phổ biến do độ dài khóa của nó. Một khóa RSA thường dài 1024 hoặc 2048 bit. Tuy nhiên, theo các chuyên gia bảo mật thì không mất nhiều thời gian để crack RSA 1024 bit, do đó nhiều tổ chức phải chuyển sang khóa 2048 bit mạnh mẽ hơn.
Hệ mật ECC (Elliptic Curve Cryptography)
Bên cạnh hệ mật RSA còn có một giải thuật khóa công khai được các chuyên gia khuyên dùng là ECC - hệ mật dựa trên đường cong Elliptic
ECC được sử dụng trong nhiều ứng dụng: chính phủ Mỹ dùng ECC để bảo vệ thông tin liên lạc nội bộ, các dự án Tor sử dụng để giúp đảm bảo ẩn danh, đây cũng là cơ chế được sử dụng để chứng minh quyền sở hữu trong Bitcoins, cung cấp chữ ký số trong dịch vụ iMessage của Apple, để mã hóa thông tin DNS với DNSCurve và là phương pháp tốt để xác thực cho các trình duyệt web an toàn qua SSL/TLS.
ECDSA (Thuật toán Chữ ký số Elliptic Curve) dựa trên DSA là một phần của mật mã đường cong Elliptic. Chính thuật toán ECDSA đã làm hệ mật ECC trở nên hữu ích cho bảo mật.
- Để thiết lập sơ đồ chữ ký ECDSA, cần xác định các tham số: lựa chọn đường cong E trên trường hữu hạn với Fp đặc số p sao cho phù hợp và công khai cho tất cả mọi người, điểm cơ sở thuộc E(Fp)
Một số khuyến nghị khi lựa chọn các tham số:
1. Kích thích q của trường, hoặc q=p(p>2) hoặc q=2^m.
2. Hai phần tử a,b thuộc Fp xác định phương trình đường cong Elliptic:
y^2 = x^3 + ax + b (p>2) hoặc y^2 + xy = x^3 + a(x^2) +b (p=2)
3. Hai phần tử xG và yG thuộc Fp xác định điểm cơ sở G=(xG,yG).
4. Bậc n của điểm G với n > (2^160) và View attachment 9406
Tạo khóa
1. Chọn số ngẫu nhiên dA trong khoảng [2,n-1] làm khóa bí mật.
2. Tính QA = dG làm khóa công khai
Hình 2. Mô hình sử dụng thuật toán mã hóa ECC trong chữ ký số
Dưới đây là mô tả chi tiết về quá trình mã hóa và giải mã trong mô hình trên.
Thuật toán ký trên bản rõ m (Quá trình mã hóa)
Người dùng A ký lên thông điệp m theo các bước sau:
Bước 1: Chọn một số ngẫu nhiên k, 2 <= k <= n-1,
Bước 2: Tính kG = (x1,y1)
Bước 3: Tính r = x1 mod n. Nếu r = 0 , quay lại bước 1.
Bước 4: Tính s = (k^(-1))(m+dr) mod n .Nếu s =0, quay lại bước 1.
Chữ ký trên thông điệp m là (r,s)
Thuật toán kiểm tra chữ ký (Quá trình giải mã)
Người dùng B kiểm tra chữ ký (r,s) trên thông điệp m theo các bước sau:
Bước 1: Kiểm tra r và s có là các số tự nhiên trong khoảng [2,n-1] không.
Bước 2: Tính w = (s^(-1)) mod n.
Bước 3: Tính u1 = mw mod n và u2 = rw mod n.
Bước 4: Tính X = (u1)G + (u2)Q = (xX,yY).
Bước 5: Nếu X=0 thì phủ nhận chữ ký. Ngược lại tính v = xX mod n.
Bước 6: Chữ ký chỉ được chấp nhận nếu v = r.
Hiện nay, hệ mật RSA là giải thuật khoá công khai được sử dụng phổ biến nhất, nhưng hệ mật dựa trên đường cong Elliptic (ECC) có thể thay thế cho RSA bởi mức an toàn và tốc độ xử lý cao hơn.
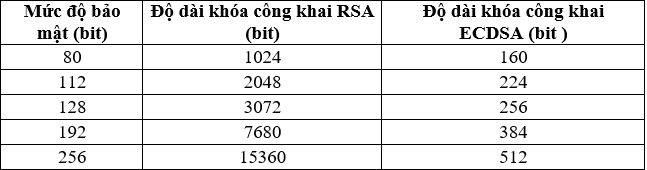
Dưới đây, là bảng so sánh các kích thước khóa RSA và ECDSA với cùng mức độ bảo mật.
Chú thích :
- Mức độ bảo mật ở đây được định lượng bởi số bit khóa tiêu chuẩn trên lý thuyết cần sử dụng để đảm bảo độ bảo mật của n bit.
- Độ dài khóa công khai cũng được đo bằng bit, nhưng nó là một khái niệm hoàn toàn khác, đề cập đến độ dài vật lý của chìa khóa.
Rõ ràng với mức độ bảo mật như nhau thì độ dài khóa của ECDSA là nhỏ hơn so với RSA. Từ đó làm tăng tốc độ xử lý một cách đáng kể, do số phép toán dùng để mã hoá và giải mã ít hơn và yêu cầu các thiết bị có khả năng tính toán thấp hơn, nên giúp tăng tốc độ và làm giảm năng lượng cần sử dụng trong quá trình mã hoá và giải mã.
Hình 3. Chứng thư số của trang web google.com.vn
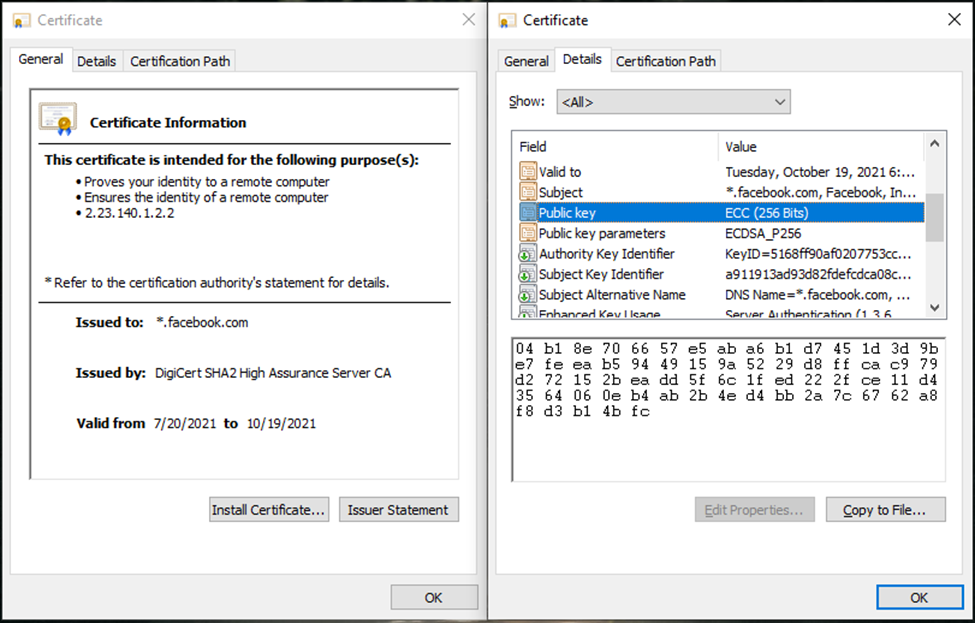
Hình 4. Chứng thư số của trang web www.facebook.com
Dễ dàng thấy được sự cải tiến của của ECDSA khiến hiệu suất của loại mã khóa này tốt hơn hẳn so với RSA, với sự cải thiện này chỉ một vài năm tới ECC sẽ là giải thuật trao đổi khoá công khai được sử dụng phổ biến nhất. Có thể nói ECC chính là hệ mật mạnh nhất hiện nay và cũng là ứng viên sáng giá để thay thế RSA trong việc tạo ra các khóa mã ngắn hơn mà vẫn đảm bảo an toàn.
Trên đây là hai loại hệ mật được sử dụng phổ biến trong việc tạo lập một chữ ký số và cả hai hê mật này đều có mức độ bảo mật cao mà các hacker ngày nay khó có thể thâm nhập được. Mong rằng bài viết này sẽ giúp các bạn có cái nhìn tổng quát hơn về RSA và ECC. Hẹn gặp các bạn trong những bài viết tiếp theo.
Chỉnh sửa lần cuối bởi người điều hành:
